Transformacja między niebieskim i ziemskim systemem odniesienia
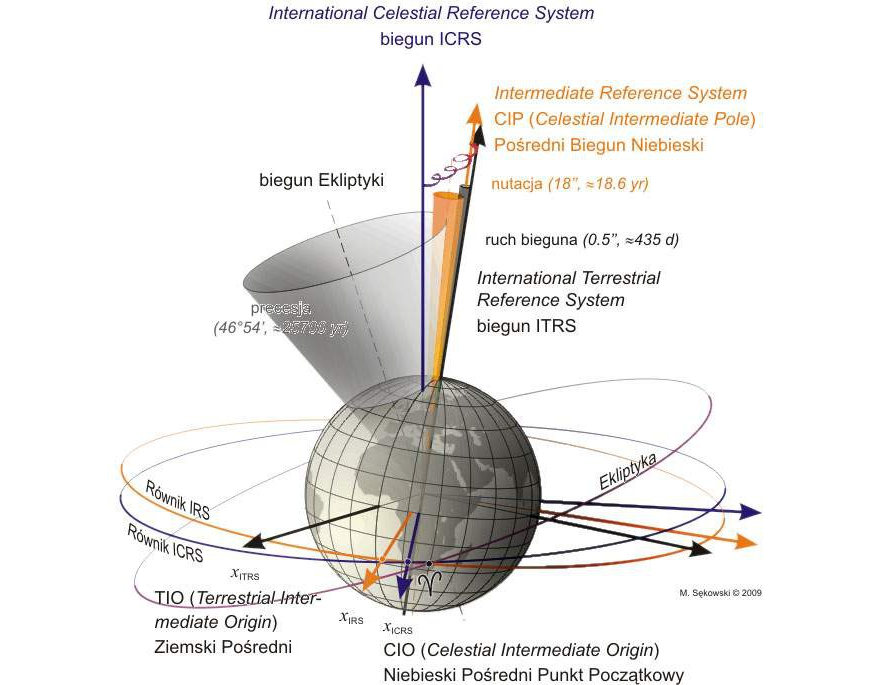 Transformacja pomiędzy ziemskim systemem odniesienia, do którego odnoszą się obserwacje, a niebieskim — quasi–inercjalnym — systemem odniesienia, w którym podawane są pozycje gwiazd, tradycyjnie jest wykonywana w trzech zasadniczych krokach.
Transformacja pomiędzy ziemskim systemem odniesienia, do którego odnoszą się obserwacje, a niebieskim — quasi–inercjalnym — systemem odniesienia, w którym podawane są pozycje gwiazd, tradycyjnie jest wykonywana w trzech zasadniczych krokach.
- W pierwszym etapie system obserwacyjny zdefiniowany przez „równik obserwacyjny” i „zerowy południk obserwacyjny” jest przeprowadzany przy pomocy parametrów opisujących ruch bieguna ziemskiego w system pośredni, zdefiniowany przez „równik pośredni” i „zerowy południk pośredni”.
- Następnym krokiem jest obrót systemu pośredniego wokół osi „równika pośredniego” o kąt reprezentujący obrót Ziemi wokół własnej osi. Obrócony w ten sposób system pośredni staje się geocentrycznym systemem niebieskim, do którego odnoszą się tzw. miejsca pozorne.
- W ostatnim kroku utworzony w poprzednim kroku system pośredni (geocentryczny system niebieski) jest przeprowadzany w system quasi–inercjalny przy pomocy parametrów opisujących precesję i nutację. W transformacji są uwzględniane dodatkowo efekty aberracji światła i paralaksy, ruch własny gwiazd i efekty relatywistyczne.
Od 1 stycznia 2003 roku, na mocy Rezolucji B1.7 IAU (Manchester, 2000), obowiązuje nowa procedura transformacji systemu ziemskiego w system niebieski. (patrz: Historia zmian pojęć i procedur...)
Jako „równik obserwacyjny” przyjmuje się równik ITRS, zaś południk zerowy ITRS odgrywa rolę „zerowego południka obserwacyjnego”. Biegunem systemu pośredniego IRS jest Pośredni Biegun Niebieski CIP, którego parametry położenia względem bieguna ITRS są obliczane w oparciu o dane dostarczane przez IERS. Transformacja ITRS do IRSZIEMSKI określa położenie TEO (dokładna realizacja chwilowego zerowego południka pośredniego) na równiku CIP zgodnie z kinematyczną definicją NRO w ITRS gdy CIP porusza się względem ITRS pod wpływem ruchu bieguna. Obrót systemu pośredniego IRS odbywa się wokół osi CIP o kąt równy Kątowi Obrotu Ziemi (ERA) będącemu liniową funkcją UT1 i przeprowadza system IRSZIEMSKI w system IRSNIEBIESKI, w którym jest określane miejsce pozorne. Uwzględnienie precesji/nutacji według teorii IAU2000 przeprowadza ten system do Geocentrycznego Niebieskiego Systemu Odniesienia (GCRS). Dodatkowo z GCRS do Barycentrycznego Niebieskiego Systemu Odniesienia (BCRS) przechodzi się przez zastosowanie post–newtonowskiej transformacji współrzędnych narzuconej przez formę odpowiednich tensorów metrycznych obu systemów (Rezolucja B1.3 IAU, 2000).
Na mocy rezolucji Zgromadzenia Generalnego IAU w Pradze, w 2006 r. dokonano jeszcze jednej modyfikacji procedury transformacji systemu ziemskiego w system niebieski. Polega ona na zastąpieniu (od 1 stycznia 2009 r.) części precesyjnej modelu precesyjno–nutacyjnego IAU2000 nową teorią precesyjną P03 (nowy model precesyjno-nutacyjny nosi nazwę IAU2006). Terminy CEO i TEO zostały przy tym zastąpione przez lepiej oddające związek z systemem pośrednim, odpowiednio: CIO — Niebieski Pośredni Punkt Początkowy i TIO — Ziemski Pośredni Punkt Początkowy.
Zależność pomiędzy wektorem jednostkowym eITRS w ITRS i jego obrazem eGCRS w GCRS wyraża się przez transformację:
eGCRS = Q(t) × R(t) × W(t) × eITRS
gdzie W(t), R(t) i Q(t) są macierzami transformacji wyrażającymi odpowiednio ruch CIP względem systemu ziemskiego ITRS, obrót systemu pośredniego IRS wokół osi CIP oraz ruch CIP względem systemu niebieskiego GCRS. Parametr czasowy t jest zdefiniowany następująco:
t = ( JD(TT) − 2000 styczeń 1d 12h TT ) / 36 525
Macierze transformacji pomiędzy systemami ziemskim i niebieskim dają się wyrazić przez iloczyn macierzy R1(ξ1), R2(ξ2) i R3(ξ3) reprezentujących obroty odpowiednio wokół osi x, y i z układu, o kąty ξ1, ξ2, ξ3 — dodatnie w kierunku przeciwnym do ruchu wskazówek zegara w przypadku stosowania układów prawoskrętnych.
Macierz W(t) ma postać:
W(t) = R3(−s') × R2(xp) × R1(yp)
gdzie xp i yp są współrzędnymi CIP w ITRS na epokę t. Wielkość s' określa spowodowaną przez ruch CIP względem ITRS zmianę pozycji TIO na równiku CIP.
Współrzędne bieguna Ziemi są zdefiniowane jako:
(xp, yp) = (xIERS, yIERS) + (Δx, Δy)tidal + (Δx, Δy)nutation
przy czym (xIERS, yIERS) są współrzędnymi bieguna dostarczanymi przez IERS (dostępne w biuletynach IERS), (Δx, Δy)tidal są składowymi pływowymi wynikającymi z pływów oceanicznych, zaś (Δx, Δy)nutation są wyłączonymi z modelu precesyjno–nutacyjnego IAU2006 składowymi nutacji wymuszonej.
Poprawki (Δx, Δy)tidal z tytułu dobowych i subdobowych efektów ruchu bieguna wywołanych pływami oceanicznymi można obliczyć korzystając z procedury dostępnej na stronach internetowych IERS. Wielkości (Δx, Δy)nutation reprezentujące dobowe i subdobowe wyrazy nutacyjne w ruchu bieguna można obliczyć korzystając z parametrów podanych w tablicy 5.1 IERS Conventions 2003.
Wielkość s' jest bardzo mała (rzędu 0.1 mas/stulecie), można ją wyznaczyć za pomocą przybliżonego wzoru:
s'(t) = −0.0015 (ac2/1.2 + aa2) t
gdzie ac i aa są średnimi amplitudami (w sekundach łuku), odpowiednio, ruchu Chandlera i rocznego w badanym okresie od t0 do t, przy czym t jest wyrażone w stuleciach juliańskich. Korzystając z aktualnych, średnich amplitud ruchów Chandlera i rocznego s' = −47 μas × t.
Macierz R(t) ma postać:
R(t) = R3(−θ)
gdzie θ jest Kątem Obrotu Ziemi (ERA).
Kąt Obrotu Ziemi oblicza się z UTC oraz dostarczanych przez IERS poprawek [UT1 − UTC]IERS, jako liniową funkcję UT1
θ(Tu) = 2π (0.779 057 273 264 0 + 1.002 737 811 911 354 48 Tu)
gdzie
Tu = JD(UT1) − 2 451 545.0
oraz
UT1 = UTC + [ UT1 − UTC ]IERS
Macierz Q(t) ma postać:
Q(t) = R3(−E) × R2(−d) × R3(E) × R3(s)
gdzie E i d są współrzędnymi sferycznymi Niebieskiego Bieguna Pośredniego (CIP) w GCRS, a parametr s jest wielkością określającą zmianę w czasie położenia Punktu Początkowego Niebieskiego Systemu Pośredniego (CIO) na równiku CIP spowodowaną przez ruch CIP względem GCRS.
Z zachowaniem dokładności na poziomie 1 μas parametr s wyraża się wzorem:
s(t) = −½ [ X(t) Y (t) − X(t0) Y(t0) ] + …
gdzie X = sin(d)·cos(E), Y = sin(d)·sin(E), Z = cos(d) są współrzędnymi kartezjańskimi CIP w GCRS, a t0 = J2000.0
Macierz Q(t) można przedstawić w funkcji współrzędnych X, Y:
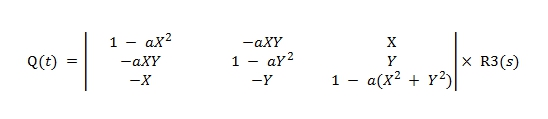
gdzie a = 1/(1 + cosd) lub z dokładnością 1 μas, a = 1/2 + 1/8 (X2 + Y2).
W praktyce współrzędne X, Y oraz wartość parametru s w modelu precesyjno–nutacyjnym IAU2006 oblicza się za pomocą sumowania składników odpowiednich szeregów, z argumentem będącym funkcją fundamentalnych argumentów teorii nutacji (argumenty Delauneya).
Współczynniki szeregów dla obliczenia współrzędnych X i Y są dostępne na stronie internetowej IERS Convention Centre.
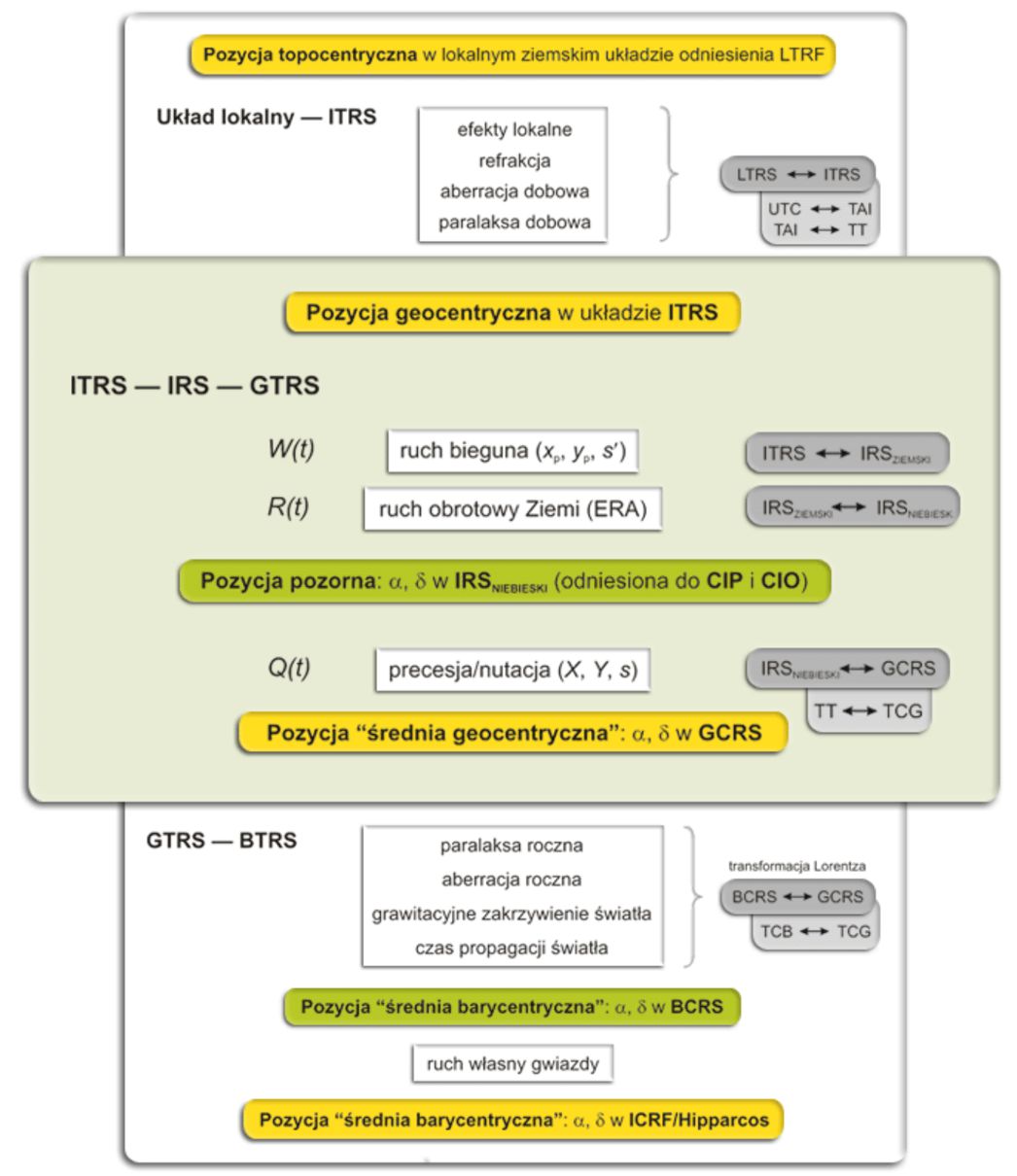
Ogólny schemat pełnej transformacji od lokalnego układu odniesienia do quasi-inercjalnego systemu niebieskiego, uwzględniający dodatkowo efekty związane z ruchem Ziemi w przestrzeni: aberracje, paralaksy itp., został przedstawiony na rysunku poniżej. Środkowa część rysunku ilustruje opisaną transformację od ITRS do GCRS.