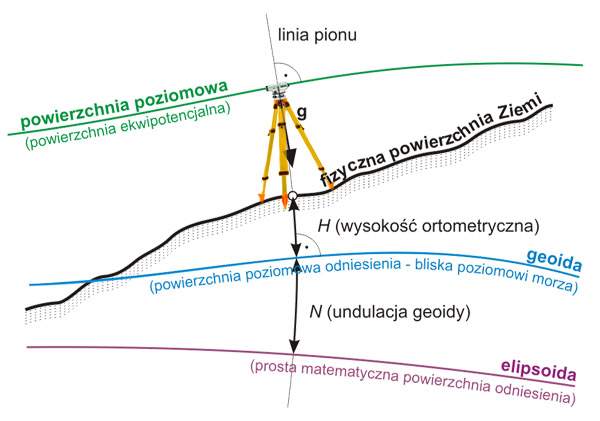
Modelowanie geoidy
 Geoida jest wykorzystywana jako powierzchnia odniesienia w systemach wysokości. Jej rola w geodezji znacząco wzrosła wraz z wprowadzeniem GPS jako powszechnie stosowanej geodezyjnej techniki pomiarowej. Wykorzystanie GPS w pomiarach wysokościowych — zamiast tradycyjnej, kosztownej i czasochłonnej, niwelacji geometrycznej — wymaga modelu geoidy o dużej rozdzielczości i wysokiej dokładności. Podobnie, wykorzystanie GPS do zagęszczania osnowy pomiarowej oraz do pomiarów sytuacyjnych wiąże się z potrzebą znajomości przebiegu geoidy. Znajomość przebiegu geoidy ściśle związana jest także z obecnymi trendami rozwoju technologii precyzyjnego wyznaczania pozycji i wysokości w czasie rzeczywistym.
Geoida jest wykorzystywana jako powierzchnia odniesienia w systemach wysokości. Jej rola w geodezji znacząco wzrosła wraz z wprowadzeniem GPS jako powszechnie stosowanej geodezyjnej techniki pomiarowej. Wykorzystanie GPS w pomiarach wysokościowych — zamiast tradycyjnej, kosztownej i czasochłonnej, niwelacji geometrycznej — wymaga modelu geoidy o dużej rozdzielczości i wysokiej dokładności. Podobnie, wykorzystanie GPS do zagęszczania osnowy pomiarowej oraz do pomiarów sytuacyjnych wiąże się z potrzebą znajomości przebiegu geoidy. Znajomość przebiegu geoidy ściśle związana jest także z obecnymi trendami rozwoju technologii precyzyjnego wyznaczania pozycji i wysokości w czasie rzeczywistym.
Powierzchnia geoidy, podobnie jak fizyczna powierzchnia Ziemi, nie daje się opisać w zwięzłej i skończonej postaci analitycznej, zachodzi więc potrzeba modelowania geoidy w formie dyskretnej.
Geoida jako powierzchnia stałego potencjału siły ciężkości Ziemi, która pokrywa się z teoretyczną powierzchnią utworzoną przez znajdujące się w stanie absolutnej równowagi oceany, jest powierzchnią utożsamianą z figurą Ziemi.
Potencjał siły ciężkości W0 na geoidzie został w ostatnich latach przyjęty jako stała fundamentalna w obowiązujących w astronomii, geodezji i geodynamice systemach odniesienia. Znajomość geoidy z odpowiednią dokładnością i rozdzielczością stanowi niezwykle ważny element, a niekiedy podstawę, rozwoju nauk o Ziemi. Za przykład może posłużyć lawinowy, w ostatnich kilku dekadach, rozwój oceanografii, klimatologii i geodynamiki, jaki następuje w wyniku możliwości monitorowania geoidy na obszarach oceanicznych z decymetrową, a następnie sub-decymetrową, dokładnością przy wykorzystaniu danych z satelitarnych misji altimetrycznych.
Działania związane z wyznaczaniem geoidy wynikają z potrzeby precyzyjnego określenia geometrycznego związku między powierzchnią Ziemi i elipsoidą odniesienia, który jest wykorzystywany w pracach geodezyjnych, geofizycznych, geologicznych i oceanograficznych.
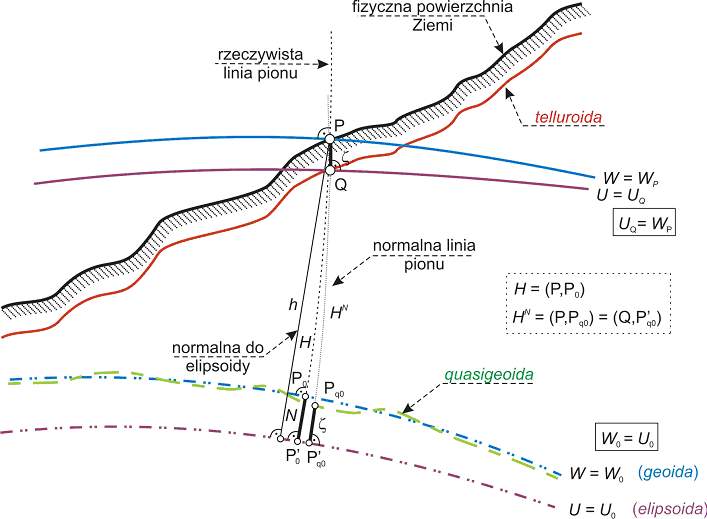 Podobnie jak geoida jest powierzchnią odniesienia dla wysokości ortometrycznych, powierzchnią odniesienia dla wysokości normalnych jest tzw. quasigeoida .
Podobnie jak geoida jest powierzchnią odniesienia dla wysokości ortometrycznych, powierzchnią odniesienia dla wysokości normalnych jest tzw. quasigeoida .
W Polsce, w praktyce stosowany jest system wysokości normalnych odniesionych do quasigeoidy. Aby z wyznaczonego odstępu geoidy od elipsoidy N uzyskać odstęp quasigeoidy od elipsoidy ζ należy wyznaczyć różnicę wysokości geoidy i quasigeoidy (N - ζ) nazywaną poprawką do geoidy, która jest prostą funkcją liniową anomalii Bouguera ΔgB. Na obszarze Polski poprawki do geoidy są rzędu centymetra i tylko w rejonach górskich osiągają wartości na poziomie decymetra.
Znajomość precyzyjnego modelu geoidy urosła do kluczowej rangi w ostatnich dekadach XX wieku z uwagi na jego zastosowanie w technikach precyzyjnego pozycjonowania przy użyciu globalnych systemów nawigacyjnych, w szczególności do wyznaczania wysokości. Precyzyjne modelowanie regionalnej geoidy stało się jednym z podstawowych zadań licznych ośrodków badawczych oraz agencji geodezyjnych.
Ze względu na rodzaju danych źródłowych wykorzystanych w modelowaniu, rozróżnia się następujące modele geoidy:
1. Model geoidy astronomiczno-geodezyjnej
gdzie danymi źródłowymi są astronomiczne odchylenia pionu, a model opracowany metodą:
- niwelacji astronomicznej — model ma formę dyskretną; wysokości geoidy wyznaczone są tylko w punktach, w których wykonano obserwacje astronomiczne i obliczono odchylenia pionu;
- kolokacji — model ma formę dyskretną; wysokości geoidy są wyznaczone w dowolnych punktach o zadanych współrzędnych.
2. Model geoidy astronomiczno-grawimetrycznej
gdzie danymi źródłowymi są astronomiczne odchylenia pionu oraz anomalie grawimetryczne użyte do wygenerowania grawimetrycznych odchyleń pionu, a model opracowany metodą
- niwelacji astronomiczno-grawimetrycznej — model ma formę dyskretną; wysokości geoidy są wyznaczone tylko w punktach, w których obliczono odchylenia pionu (astronomiczne i grawimetryczne);
- kolokacji — model ma formę dyskretną; wysokości geoidy wyznaczone w dowolnych punktach o zadanych współrzędnych.
3. Model geoidy grawimetrycznej
gdzie danymi źródłowymi są anomalie grawimetryczne, a model opracowany metodą
- całkową (Stokesa lub Molodenskiego) — model ma formę dyskretną; wysokości geoidy są wyznaczone w dowolnych punktach o zadanych współrzędnych;
- kolokacji — model ma formę dyskretną; wysokości geoidy są wyznaczone w dowolnych punktach o zadanych współrzędnych.
4. Model geoidy satelitarno-niwelacyjnej
gdzie danymi źródłowymi są, wyznaczone techniką GNSS, wysokości elipsoidalne na punktach o znanej wysokości ortometrycznej (lub normalnej) — model ma formę dyskretną; wysokości geoidy są wyznaczone tylko w punktach, w których wykonano obserwacje GNSS, i w których znana jest wysokość ortometryczna (lub normalna)
5. Model geoidy grawimetrycznej dopasowanej
gdzie danymi źródłowymi są model geoidy grawimetrycznej oraz zbiór wysokości geoidy wyznaczonych jako różnica, pomierzonych techniką GNSS, wysokości elipsoidalnych i odpowiednich, wyznaczonych przy użyciu niwelacji precyzyjnej wysokości ortometrycznych (lub normalnych) — model ma formę ciągłą.
6. Model geoidy zintegrowanej
gdzie danymi źródłowymi są, w różny sposób kompleksowo opracowane, dane kilku rodzajów (odchylenia pionu, anomalie grawimetryczne, dane GNSS wraz z danymi z niwelacji precyzyjnej) — model może mieć formę ciągłą.